Back

3.2 Use of amount of substance in relation to masses of pure substances

3.2.1 Moles

- Chemical amounts are measured in moles. The symbol for the unit mole is mol.
- Moles are 6.022 × 10^23 particles (this is known as Avogadro's number).
- The mass of one mole of a substance in grams is numerically equal to its relative formula mass, and one mole of a substance contains the same number of the stated particles, atoms, molecules or ions as one mole of any other substance.
- For example, one mole of Oxygen contains 6.022 × 10^23 atoms, and oxygen has a relative atomic mass of 16, one mole of oxygen weighs 16g.
- mass = moles * molar mass

3.2.2 Amounts of substances in equations

- The masses of reactants and products can be calculated from balanced symbol equations.
- Chemical equations can be interpreted in terms of moles. For example:
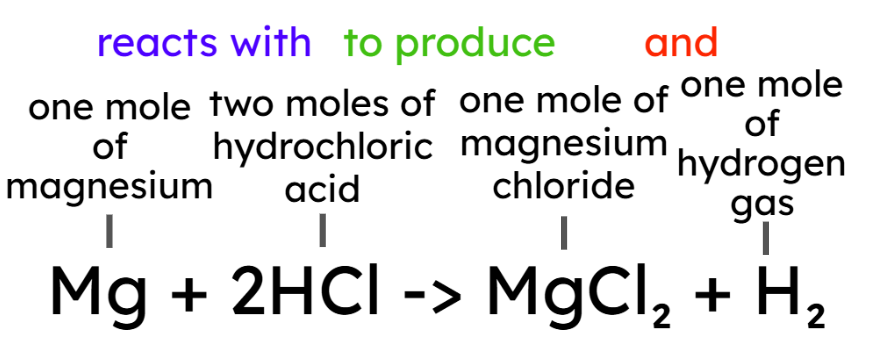- "one mole of magnesium reacts with two moles of hydrochloric acid to produce one mole of magnesium chloride and one mole of hydrogen gas."

Mole calculations (aka pain)

1. Write the balanced symbol equation.
2. Work out Mr (molar mass) for the substances you need (use periodic table values).
3. Convert the known mass to moles using moles = mass ÷ Mr.
4. Use the mole ratio from the balanced equation to find the moles of the required substance.
5. Convert moles back to mass (if the question asks for mass) using mass = moles × Mr and round to the correct number of significant figures.

Worked example 1 — forward calculation (mass of product from a mass of reactant)

Reaction: Mg + 2HCl → MgCl2 + H2
Question: If 3.00 g of magnesium reacts completely with excess hydrochloric acid, what mass of hydrogen gas is produced? (Use Mr: Mg = 24.305, H = 1.008, Cl = 35.453) [in reality in the exam you'd need to use your periodic table for this]
Solution:

1. Balanced equation already given: 1 mol Mg produces 1 mol H2 (mole ratio Mg : H2 = 1 : 1).
2. Calculate Mr for hydrogen gas (H₂): Mr(H2) = 2 × 1.008 = 2.016.
3. Convert mass of Mg to moles:
   moles(Mg) = mass ÷ Mr = 3.00 ÷ 24.305 = 0.123431392718...
4. Use mole ratio to get moles of H₂: because ratio is 1:1, moles(H2) = moles(Mg) = 0.123431392718...
5. Convert moles of H₂ to mass:
   mass(H2) = moles × Mr = 0.123431392718 × 2.016 = 0.248837687719 ≈ 0.249 g (rounded to three significant figures).

Worked example 2 — using a reactant amount to find mass of a product using limiting stoichiometry

Reaction: Mg + 2HCl → MgCl2 + H2
Question: 10.0 g of hydrochloric acid is available and reacts completely (excess magnesium). What mass of magnesium chloride is produced? (Use Mr HCl = 36.461, Mr MgCl2 = 95.211)
Solution:

1. Balanced equation: 2 mol HCl → 1 mol MgCl2 (mole ratio HCl : MgCl2 = 2 : 1).
2. Convert mass of HCl to moles:
   moles(HCl) = 10.0 ÷ 36.461 = 0.274265653712...
3. Convert moles of HCl to moles of MgCl2 using the mole ratio:
   moles(MgCl2) = moles(HCl) × (1 mol MgCl2 / 2 mol HCl) = 0.274265653712 ÷ 2 = 0.137132826856...
4. Convert moles of MgCl2 to mass:
   mass(MgCl2) = moles × Mr = 0.137132826856 × 95.211 = 13.0565535778 ≈ 13.1 g (rounded to three significant figures to match 10.0 g).

Worked example 3 — reverse calculation (find required mass of reactant)

Reaction: 2H2 + O2 → 2H2O
Question: How much oxygen (O₂) is needed to completely react with 5.00 g of hydrogen gas? (Use Mr H2 = 2.016, Mr O2 = 32.00)
Solution:

1. Balanced equation gives mole ratio H₂ : O₂ = 2 : 1 (2 mol H₂ react with 1 mol O₂).
2. Convert mass of H₂ to moles:
   moles(H2) = 5.00 ÷ 2.016 = 2.480158730158...
3. Use mole ratio to find moles of O₂ required:
   moles(O2) = moles(H2) × (1 mol O2 / 2 mol H2) = 2.480158730158 ÷ 2 = 1.240079365079...
4. Convert moles of O₂ to mass:
   mass(O2) = moles × Mr = 1.240079365079 × 32.00 = 39.682539681 ≈ 39.7 g (three significant figures).

3.2.3 Using moles to balance equations

- The balancing numbers in a symbol equation can be calculated from the masses of reactants and products by converting the masses in grams to amounts in moles and converting the numbers of moles to simple whole number ratios.

Example

Question: When 8.0 g of methane (CH₄) burns in excess oxygen, 22.0 g of carbon dioxide (CO₂) and 9.0 g of water (H₂O) are produced. Use moles to balance the equation for this reaction.
Unbalanced equation: CH4 + O2 → CO2 + H2O
Solution:

1. Calculate moles of each substance using their masses and relative formula masses:
   Mr(CH₄) = 12.01 + (4 × 1.008) = 16.042
   Mr(CO₂) = 12.01 + (2 × 16.00) = 44.01
   Mr(H₂O) = (2 × 1.008) + 16.00 = 18.016
2. Moles of CH₄: 8.0 ÷ 16.042 = 0.499
   Moles of CO₂: 22.0 ÷ 44.01 = 0.500
   Moles of H₂O: 9.0 ÷ 18.016 = 0.499
3. Write the ratio of moles (approximate to whole numbers):
   CH₄ : O₂ : CO₂ : H₂O = 0.5 : ? : 0.5 : 0.5
   (O₂ is in excess, so not calculated here)
4. Simplify the ratio to whole numbers:
   CH₄ : CO₂ : H₂O ≈ 1 : 1 : 1
5. Balance the equation using these ratios and add O₂ to balance oxygen atoms:
   CH4 + ?O2 → CO2 + 2H2O
CH4 + 2O2 → CO2 + 2H2O

3.2.4 Limiting reactants

- In a chemical reaction involving two reactants, it is common to use an excess of one of the reactants to ensure that all of the other reactant is used.
- This means that more of one reactant is present than is needed to completely react with the other reactant – this is the one in excess.
- The reactant that is completely used up is called the limiting reactant because it limits the amount of products.

How to find the limiting reactant

- Sometimes the limiting reactant is obvious, but in a GCSE exam you're likely to be asked to calculate it using moles.
- To find the limiting reactant, follow these steps:

1. Write the balanced equation for the reaction.
2. Calculate the number of moles of each reactant.
3. Use the mole ratios from the balanced equation to determine which reactant is limiting.

Worked Example

- Consider the reaction between nitrogen (N₂) and hydrogen (H₂) to form ammonia (NH₃): - Say there is 12.0g of nitrogen and 7.0g of hydrogen.
- First, we need to write the balanced equation:
- N2 + 3H2 → 2NH3
- Next, we calculate the moles of each reactant:
- 12.0 (mass) ÷ 14 * 2 (A_r and amount of atoms) = 12/28 = 0.426 moles of nitrogen
- 7.0 (mass) ÷ 1 * 2 (A_r and amount of atoms) = 7/2 = 3.5 moles of hydrogen
- Finally, we need to find the molar ratios:
- From the balanced equation, we see that 1 mole of N₂ reacts with 3 moles of H₂ to produce 2 moles of NH₃.
- Therefore, the molar ratio is:
- N₂ : H₂ : NH₃ = 1 : 3 : 2
- Therefore, nitrogen is the limiting reactant (0.426 is smaller than 1.17 (3.5 ÷ 3), therefore nitrogen is limiting)

3.2.5 Concentration of solutions

- Many chemical reactions take place in solutions.
- The concentration of a solution can be measured in mass per given volume of solution, e.g. grams per dm³ (g/dm³).
- Concentration (g/dm³) = mass of solute (g) / volume of solution (dm³)

How to calculate mass of solute in a given volume

1. Write down the concentration and volume of the solution.
2. Rearrange the formula to find mass: mass = concentration × volume
3. Make sure the volume is in dm³ (1 dm³ = 1000 cm³).
4. Multiply the concentration by the volume to get the mass of solute.

Worked example

Question: What is the mass of sodium chloride (NaCl) dissolved in 250 cm³ of solution with a concentration of 2.0 g/dm³?
Solution:

1. Convert volume to dm³: 250 cm3 ÷ 1000 = 0.250 dm3
2. Use the formula: mass = concentration × volume
3. Calculate: mass = 2.0 g/dm3 × 0.250 dm3 = 0.50 g

Relationship between mass, volume, and concentration

- The concentration of a solution tells you how much solute is dissolved per unit volume.
- If you increase the mass of solute while keeping the volume the same, the concentration increases.
- If you increase the volume while keeping the mass of solute the same, the concentration decreases.
- The formula concentration = mass / volume can be rearranged to find any variable:

• mass = concentration × volume
• volume = mass / concentration